【PAPER.0x01】论文笔记：Hunting the Haunter — Efficient Relational Symbolic Execution for Spectre with Haunted RelSE

鬼！

0x00.一切开始之前

本校在毕设之前还有个“小毕设”——网络空间安全综合实验 ，刚好笔者要做的题目是基于这篇论文完成的，所以还是简单写一个阅读笔记：）

说是笔记，其实还是差不多相当于把原文翻译了一遍（（（

Abstract

Spectre 是一种微架构层面的漏洞，其允许攻击者利用推测执行（speculation executino）技术中的漏洞来泄露信息，但对于该类型漏洞的检测面临着两个挑战：①推测路径带来的搜索空间爆炸②在不同编译阶段引入的 Spectre 漏洞

本文提出了在二进制级的 Spectre 漏洞的量化检测的优化方法：Haunted RelSE，并证明了相比于在最先进的工具中的更朴素的显式推测执行方法（more naive explicit speculative execution approach），该优化是语义正确的

研究者在一个符号分析工具中应用了 Haunted RelSE ，并在一个有名的 Spectre-PHT（Spectre v1） 的 litmus tester 上进行了测试，并打算在一个新的 Spectre-STL（Spectre v4）的 litmus tester 上测试

litmus test：对内存一致性的测试

好像没有啥中文翻译，相关的中文资料也少，摸了

该技术比最先进的工具发现了更多的 violations 与 scales，并让研究者发现：对 Spectre-PHT 的标准防护手段 index-masking 与著名的编译 位置无关的可执行文件 （position independent executables）的 gcc 选项，导致了 Spectre-STL 的引入

研究者提出并验证了一种对 index-masking 的修正方法

0x01. INTRODUCTION

现代 CPU 的执行速度依赖于包括分支预测器（branch predictor）与 投机 （ speculation ）在内的复杂硬件逻辑：提前执行指令 & 尝试通过分支预测器来推测执行（speculatively execute）一条控制流，若推测失败则恢复被影响区域——称为 恢复执行 （Reverted execution，也叫做 瞬态执行 （transient execution），意为从架构角度来看这个操作是透明的）

但瞬态执行会在微架构级（microarchitecture）留下可观测的侧面影响（side effects），而这可以被攻击者用以恢复架构级（architectural）的秘密——这种攻击手法称之为幽灵攻击（Spectre attacks）

幽灵有着多种变种，但绝大部分的工作都仅关注于 Spectre-v1 （Pattern History Table，对条件分支的攻击），仅有 Pitchfork 做了 Spectre-v4 （Store to Load，对内存屏障预测器的攻击）的相关工作，但并不完善

Goal and Challenge

本篇论文中研究者提出了一种用以检测 Spectre-PHT 与 Spectre-STL 漏洞的方法，并应用于静态二进制代码分析中，这面临着两个挑战：

• C1：微架构的细节在分析中无法被完全获得，需要一种足够强大的提取方法以提取造成侧信道攻击的微架构状态（mocroarchitectural state）
• C2：对可能的推测执行的探索的规模不能太大，否则会造成状态爆炸（state explosion）

Proposal

本文通过在文献中创造的 关系安全属性 （relational security property）作为 推测常数时间 （speculative constant-time）来应对挑战 C1。推测常数时间在没有详细建模复杂的微架构细节的情况下将推测执行纳入考虑，但编译器没必要保护常数时间编程（constant-time programming），故我们的分析在二进制层操作（无需源码）。本文将前人的模型扩展到常数时间二进制分析上，以分析 推测常数时间

符号执行（symbolic execution）是一项在二进制代码上扩展良好的技术，但为了分析推测常数时间，其必须考虑程序的推测行为。Spectre-PHT 与 Spectre-STL 的符号分析者通过 fork 以探索临时路径，从而对推测性行为进行 清晰地 （explicitly）建模，而这导致了状态爆炸——尤其是对 Spectre-STL 而言。对符号执行的常数时间样式（constant-time-like）的属性的改造，称为 关系符号执行 （relational symbolic execution， RelSE），在二进制层面的可伸缩性与精度上已被证明是非常成功的

为了解决 C2，本文的核心技术是利用 RelSE 来 在同一时间 像常规执行（即，与正确的推测相关的执行） 那样执行临时的执行；本文将这种技术命名为 Haunted RelSE：

• 对于 Spectre-PHT，其通过同时执行由条件语句产生的瞬态的与常规的路径以对多余状态进行剪枝
• 对于 Spectre-STL，其对多余状态进行剪枝并将剩余部分编码在一个单独的符号路径中，而非为每个可能的加载与存储交叉将符号执行进行分支

本文在一个二进制层的关系符号分析工具 BINSEC/HAUNTED 中应用 Haunted RelSE，为了进行评估，本文使用了 Spectre-PHT 的著名测试用例 Kocher ，以及一组为 Spectre-STL 提出的新测试用例，以及来自 donna、Libsodium 与 OpenSSL 库的真实世界密码学代码

Findings. 本文的工作展示了一种用于对抗 Spectre-PHT 的著名防御手段 index-masking 可能会引入新的 Spectre-STL 漏洞，并提出且验证了用以解决这个问题的安全实现，通过本文的工具还发现了 GCC 中一个流行的用以生成位置无关代码（position-independent code）的选项可能引入 Spectre-STL 漏洞，同时还确认了由编译器添加的栈保护在密码原语（cryptographic primitives）中引入了 Spectre violations

Contributions. 总结起来本文的工作就是：

• 研究者设计了一种基于关系符号执行的技术，称之为 Haunted Relse，用以在符号分析中高效地分析推测执行，以检测 PHT 与 STL Spectre（Section III & IV）；Haunted Relse 的基本思想是同时基于常规的与瞬态的行为进行符号化推断，尽管研究者对内存的编码让人联想到一些状态合并的编码，但实际上其遵循了不同的理论，通过防止常规与瞬态执行之间的人工阻断，而非试图将不同的路径（可能不相关）打包在一起；研究者正式证明了显式地对所有的推测路径建模进行关系分析与使用 Haunted Relse 在语义上等价（Section IV）
• 研究者提出了一种名为 BINSEC/HAUNTED 的验证工具，实现了 Haunted Relse，并通过著名的用于 spectre-PHT 的 litmus test 进行评估；研究者还进一步地提出一组用于 Spectre-STL 的 litmus test 且用其测试了 BINSEC/HAUNTED；试验的评估显示了 BINSEC/HAUNTED 可以在如 OpenSSL、donna、Libsodium 这样的真实世界的密码学代码中发现推测常数时间漏洞；对于 Spectre-PHT，BINSEC/HAUNTED 最多可以分析 5k 条静态指令，并比现有水平的 KLEESpectre 与 Pitchfork 更快（但精准度更低）；对于 Spectre-STL，其可以最多分析 100 条指令并在高达 6k 条指令的代码中找到漏洞；相比于 Pitchfork，BINSEC/HAUNTED 明显更快，且能找到更多的漏洞并报告更多的不安全程序
• 据研究者所知，其第一个报告了著名的用于对抗 Spectre-PHT 的防护 index-masking 有可能引入 Spectre-STL 漏洞；研究者提出了用以修复这个问题的正确实现（Section VI），并用其工具进行了验证；研究者同时还第一个报告了 GCC 编译器的 PIC 选项引入了 Spectre-STL 漏洞（Section VI）

Discussion. 当 Spectre attacks 开启了系统安全的新战场，对推测执行的思考变得困难且冗长，这需要自动搜索技术，但由于额外的推测行为引起的路径爆炸，此前的提案都存在可扩展性问题，Haunted RelSE 是向着可扩展的对 Spectre attacks 的分析迈出的一步；对于 Spectre-PHT，Haunted RelSE 可以在一些情况下提高分析速度，对分析推测语义的复杂性进行剪枝，并缩放于中等大小的真实世界中的密码学二进制文件；对于 Spectre-STL，其为第一个可以彻底分析小的真实世界密码学二进制文件的工具，并能在中等大小的真实世界密码学二进制文件中找到漏洞

0x02. BACKGROUND

本节研究者提供了关于 Spectre 的基本背景：推测常数时间（speculative constant-time）与关系符号执行（relational symbolic execution）

Spectre attacks. 在现代处理器中，只要指令的操作数可用，其被按顺序获取并存放在一个 重排序缓冲区 （reorder buffer）中，且能按任意顺序执行；处理器同时使用推测（speculation）机制以在特定指令执行之前预测其输出，由误判带来的指令流——即 瞬态执行 （transient execution）会被在架构级还原（例如恢复寄存器的值），但这可能遗留微架构级的侧面影响（例如 cache 的状态可能不会被恢复），而这些微架构级的侧面影响对程序是透明的，这使得攻击者可以进行侧信道攻击，幽灵攻击（Spectre attacks） 便是利用这种推测机制来触发这样的会在微架构级存储秘密数据的瞬态执行——称之为 spectre gadgets，这将被通过侧信道攻击进行复原

幽灵攻击一共有四种根据针对的机制的不同变种：

• Spectre-PHT：对用以预测条件分支的 Pattern History Table 进行利用
• Spectre-BHB：对用以预测分支地址的 Branch Target Buffer 进行利用
• Spectre-RSB：对用以预测返回地址的 Return Stack Buffer 进行利用
• Spectre-STL：对用以预测 Store-To-Load dependencies 的消歧义机制进行利用

对 BTB 与 RSB 变种的推测机制，可能会被误认为任意地址跳转，这对静态分析而言比较棘手（参见 Section VII），故研究者主要关注 Spectre-PHT 与 Spectre-STL

Spectre-PHT. Pattern History Table 用以在微架构级预测条件分支的输出；我们首先介绍 Spectre 的变种 1，攻击者滥用分支预测器以故意在一个分支进行错误的推测；即使程序中的条件语句在架构级确保了内存访问的范围固定，攻击者可以引导 PHT 错误预测一个分支的值以瞬态执行一个越界内存访问，这在缓存中留下可以被观测到的且能被用以恢复越界读的数据的影响（Listing 1）

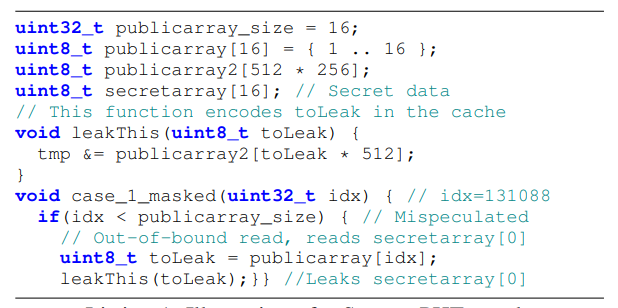
Spectre-STL. Store-To-Load dependencies 需要在所有的 store 指令完成执行前 load 指令不会执行，为了让 CPU 瞬态执行 store 指令并避免缓存未命中导致的暂停，store 指令以队列形式存放在一个 store buffer 中，而相较于等待先前的 store 指令完成，load 指令可以直接从匹配的带有 store-to-load forwarding 的 store buffer 中取值；此外，当内存消歧义器（memory disambiguator）预测到一个 load指令并非等待中的 store 的别名，其可以 推测性地绕过在 store buffer 中等待中的 store 并直接从主存取值；Spectre-STL 利用这种行为来载入会被编码于缓存中的包含秘密数据的旧值（Listing 2）

Speculative constant-time（SCT）. 常数时间（constant time）是密码学代码中一个流行的编程规范：程序不会存储、装载秘密数据值或是以其进行分支，以避免侧信道数据泄露；然而常数时间并不足以预防幽灵攻击，如 Listing 1 为一个常规的没有对秘密数据的访问或以其分支的常数时间程序，但该程序存在 Spectre-PHT 漏洞，攻击者可以误导式训练分支预测器并在瞬态执行中泄露秘密数据；推测常数时间是最近的一个扩展常数时间以考虑瞬态执行的安全属性

Definition 1（Speculative constant-time）. 当且仅当一个程序的每一对（推测）执行有着相同的公共输入并协定了推测决策、且互相的控制流与内存访问都相等时，该程序关于推测常数时间是安全的。

需要注意的是 SCT（类似于常数时间与其他信息流属性）并非一个执行轨迹的属性，而与两个执行轨迹相关联，因此需要近似工具以高效地建模轨迹对

Binary-level symbolic execution. 符号执行（Symbolic Execution）即使用符号输入执行程序，其会构建一个称为 路径谓语 （path predicate）的逻辑表达式，用以保存在执行过程中遇到的分支条件；为了确认一条路径是否能通，路径谓语会被交给可满足性模理论求解器（SMT solver）进行求解；符号执行同时还能检查断言以寻找漏洞或是进行有界验证（即，在一个确定的深度下进行验证）

分析二进制代码通常采用将代码指令解码为一种低级的中间语言的形式，在二进制级的符号执行中的值（如寄存器、内存地址、内存内容等）为固定大小的符号位向量，内存被表示为一个用 32 位的位向量表示地址的符号字节数组，一个符号数组为一个通过如下操作将每个下标 i ∈ I 映射到对应值 v ∈ V 的函数（Array I V）：

• select：(Array I V) × I → V 获取一个数组 a 与一个下标 i，返回一个存储在数组 a 的下标 i 的值 v
• store：(Array I V) × I × V → (Array I V) 获取一个数组 a 、一个下标 i 与一个值 v，返回将下标 i 映射到值 v 的数组 a

Relational Symbolic Execution. 关系符号执行（RelSE）是一种有前景的将符号执行进行扩展以分析如 SCT 这样的两个执行路径的安全属性的方法，其符号化地在相同的符号执行实例中执行一个程序的两个版本并在其之间最大化共有部分；以分析常数时间为例，RelSE 让两个程序 共享相同的公有输入 （public input），但使用不同的 秘密输入 （secret input），并在执行过程中检查是否条件分支的输出与内存下标在两个执行中必须一致——这代表其是否决定于秘密

在 RelSE 中，变量被映射到 关系表达式 （relational expression）中，当其可能依赖于秘密数据时，其为一对符号表达式（表示为 <ϕl | ϕr> ），否则为一个简单的符号表达式（表示为 <ϕ> ）；为了对内存访问与条件指令进行安全评估，研究者使用如下定义的函数 secLeak 以确保一个关系表达式并不决定于秘密（即，表达式左右内容必须相等）：

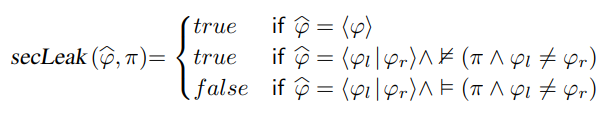
|= 表示可满足（反之表示不满足），其依赖于这样一个事实：若 $\widehat{\varphi}$ 为一个简单的表达式，参照定义，其并不依赖于秘密，因而可以被安全地泄露；然而若 $\widehat{\varphi}$ 为一对表达式 <ϕl | ϕr> ，仅当 ϕl 与 ϕr 在当前路径谓语 π 下不可被确认时（即表达式 π ∧ ϕl ≠ ϕr 不可被满足），泄露才是安全的

Notations. 大小为 n 的符号位向量的集合表示为 Bv_n ，符号表达式（位向量或数组） ϕ, ϕl , ϕr, ψ, . . . 的集合表示为 Φ ，关系表达式 $\widehat{\varphi}$，$\widehat{\psi}$, . . . 的集合表示为 Φ ， $\widehat{\varphi}$ 左、右的值表示为 $\widehat{\varphi _{|l}}$ 、$\widehat{\varphi _{|r}}$ ，若$\widehat{\varphi} = \langle \varphi \rangle$ ，则 $\widehat{\varphi _{|l}}$ 、$\widehat{\varphi _{|r}}$ 都被定义为 $\widehat{\varphi}$ ，符号数组上的函数 select 与 store 的关系表达式为：

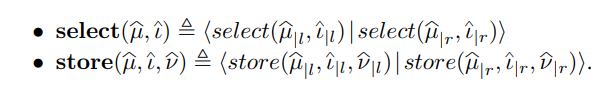
0x03. HAUNTED RELSE

为了分析 SCT，我们需要修改 RelSE 以考虑程序的推测语义（speculative semantics），这包括 常规表达式 ——被作为一个好的推测结果而执行的且会在推测被解决时保存的指令——以及所有可能的 瞬态执行 ——被作为误测且会在推测解决时被丢弃的指令；本节描述解决这个问题的方法——在最新的工具中使用（参见 Table V）——研究者称之为 Explicit ，因为其直接建模了瞬态执行，并展现了研究者的优化探索策略，称之为 Haunted

A. Spectre-PHT

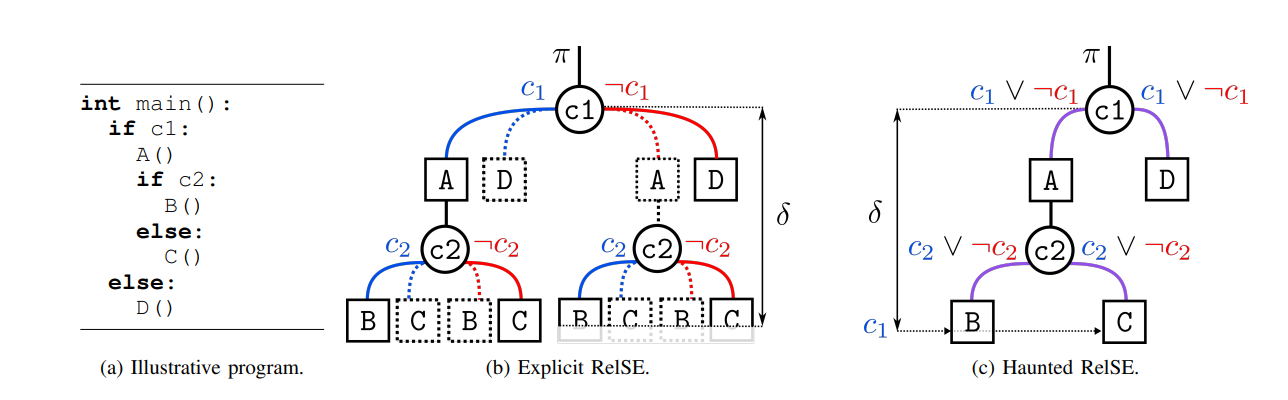
1）Explicit RelSE for Spectre-PHT ： Explicit 尝试通过符号执行建模 Spectre-PHT——于 KLEESpectre 中引入——通过将每个条件分支分成四个路径来直接地建模了瞬态执行；例如 Fig.1a 中的程序与 Fig.1b 中的该程序的符号执行树，在条件指令 if c1 后，执行将分成四个路径：

• 两个 常规路径 （regular path）：如同标准符号执行一般，第一个路径跟着 then 分支并将约束 (c1 == true) 添加到路径谓语中，第二条路径跟着 else 分支并将约束 (c1 == false) 添加到路径谓语中
• 两个 瞬态路径 （transient path）：为了统计被误判到 true 的瞬态执行，then 分支被以约束 (c1 == false) 执行，为了统计被误判到 false 的瞬态执行，else 分支被以约束 (c1 == true) 执行；这些瞬态路径会在达到 推测边界 （speculation bound，通常由重排序缓冲区的大小决定）后被丢弃

为了验证 SCT，我们需要确认内存访问与条件状态是否在常规路径与瞬态路径上都没有泄露秘密信息；在常规路径上我们要确认程序的 控制流 与 load 和 store 指令的下标 并不决定于秘密输入，然而在瞬态路径上我们仅确认 控制流 与 load 和 store 指令的下标 ，因为在推测执行中，内存的 store 操作为 store buffer 中的队列，直到过期之前对缓存都不可见

Problem with Explicit ：对于 Fig. 1b，我们看到两条子树都为常规执行与瞬态执行 then 分支的结果（即 子树起始于状态 A ），对应于不同路径谓语下的相同指令，准确地说，若我们将 $\widehat{\psi _{cf} }$ 、$\widehat{\psi _{ld} }$ 、$\widehat{\psi {st}}$ 称为子树 A 中对应的 控制流状态、 load 下标、store 下标 的关系表达式，则对于常规执行我们需要检查 $seckeak(\pi \and c{1},\widehat{\psi {cf}}) \and seckeak(\pi \and c{1},\widehat{\psi {ld}}) \and seckeak(\pi \and c{1},\widehat{\psi {st}})$ ，对于瞬态执行我们需要检查 $seckeak(\pi \and \neg c{1},\widehat{\psi {cf}}) \and seckeak(\pi \and \neg c{1},\widehat{\psi _{ld}})$；最终等价于检查如下表达式：

$$
seckeak(\pi,\widehat{\psi _{cf}}) \and seckeak(\pi,\widehat{\psi {ld}}) \and seckeak(\pi \and c{1},\widehat{\psi _{st}})
$$

该表达式基本近似于在没有约束 c1 的情况下符号化地执行 then 分支至 $\delta$，检查 load 的下标 $\widehat{\psi _{ld} }$ 与控制流表达式 $\widehat{\psi _{cf} }$，仅将 c1 添加到 store 下标 $\widehat{\psi _{st} }$ 的检查中

这样的发现让研究者设计出来 Explicit RelSE 的优化方法：探索一个单独的同时包含程序的常规与瞬态行为的推测路径，以在保存一个等价结果的同时对状态进行剪枝

2）Haunted RelSE for Spectre-PHT ：相较于将执行分为四个路径，Haunted RelSE 仅将其分为两个路径，如 Fig. 1c 所示，在条件分支 if c1 之后，执行将分为两个路径：一个路径跟随 then 分支（子树 A），另一路径跟随 else 分支（子树 B），两个分支都同时对常规与相应的瞬态路径的行为进行建模；此外，其会延迟（可能免去）对路径约束的检查——仅会添加约束 $c _{1} \or \neg c _{1}$ ；最终，约束将会在条件分支失效后（在 $\delta$ 步后）被添加到路径谓语中

在每个条件状态 （或是 load 指令），研究者会检查条件（或是 load 下标）在常规执行与瞬态执行中都不依赖于秘密（即，使用路径谓语 π）：$seckeak(\pi,\widehat{\psi _{cf}}) \and seckeak(\pi,\widehat{\psi _{ld}})$ ；另一方面，store 指令仅会在常规执行下被检查（即，使用路径谓语 $\pi \and c _{1}$）；最终，条件 $(c1 == true)$ 会被在 $\delta$ 步后被添加到路径谓语中

B.Spectre-STL

1) Explicit RelSE for Spectre-STL ：在微架构级别，一个 load 指令可以从 store buffer 的任意匹配的 entry 或是从主存获取其值，这意味着 load 可以绕过 store buffer 中未决的 store 操作直到达到主存；为了统计这一行为， Explicit 策略——应用于 PITCHFORK 中——通过为每个可能的 load 与 store 交错进行符号执行分支以直接建模瞬态执行

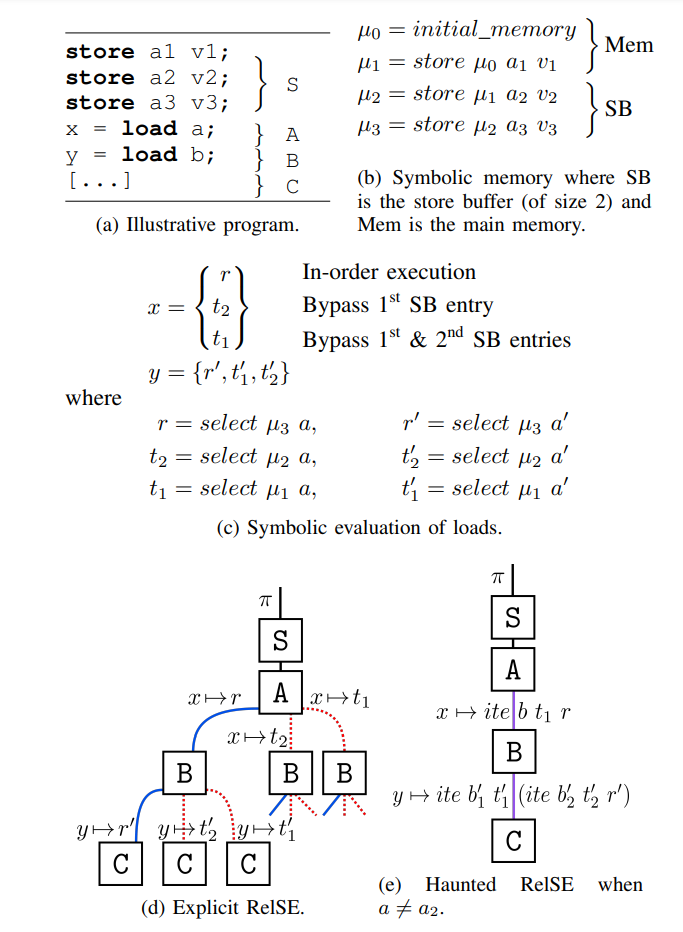
考虑 Fig.2a 中的程序，对于 store 指令的符号执行给出 Fig. 2b 中定义的符号化内存 $\mu _{3}$，其为从 initial_memory 开始的一系列符号化 store 操作；有了这样按时间顺序的表示，我们可以很容易地用符号化内存中的最后 |SB| 次 store 操作来定义一个大小为 |SB| 的 store buffer；类似的，主存也可以通过移除符号化内存中的最后 |SB| 次 store 操作进行定义；以一个大小为 2 的 store buffer 为例，当主存由 $\mu _{1}$ 定义时，最后两次 store 构成了 store buffer

第一条 load 指令（block A）可以绕过 store buffer 中的每一个 store 操作直到其达到主存，因此 x 有三种可能的值，如 Fig. 2c 所示：

• 常规值 $r$ 对应一个最近的符号化内存 $\mu _{3}$ 的符号化的 $select$ 操作，因为所有先前的 store 操作都被按顺序编码进了 $\mu _{3}$ ，这对应着顺序执行
• 第一个瞬态值 $t _{2}$ 通过绕过 store buffer 中的第一个 entry 而获得，这对应着 $\mu _{2}$ 中的一个符号化 $select$ 操作
• 最后一个瞬态值 $t _{1}$​ 通过绕过 store buffer 中的第一与第二个 entry 并从主存取值而获得，这对应着 $\mu _{1}$ 中的一个符号化 $select$ 操作

类似地，变量 y 同样有三种可能的取值

如 Fig. 2d 中所示的 Explicit 探索策略为 load 的每个能获取的可能的值进行符号执行分支，这将很快导致路径爆炸，我们通过实验表明（Section V-C）即便是在较少代码上（100条指令）这个问题也很难解决

2) Haunted RelSE for Spectre-STL ：研究者首先观察到大部分路径都是多余的，一个 load 可以通过先前的非别名 store 进行代偿，考虑 Fig. 2c 中的评估，若我们能够确认 load 的下标 $a$ 与第二个 store 的下标 $a _{2}$ 不同，根据数组的定义，我们有 $t _{2} = t _{1}$ ，由此路径 $x \to t _{2}$ 与其所有的子路径都是多余的； 研究者基于一种著名的称之为 read-over-write 的对符号数组的优化来检测与剪枝多余的情况 （cases）

然而，对多余情况的合并并不足以解决路径爆炸（参见 Section V），由此 研究者提出一种新的编码以在一个单独的路径谓语中保存剩下的情况 ，其使用符号化的 if-then-else 来在一个单独的表示中编码所有可能被 load 取的值，而非为每个可能的情况进行分支执行

例如 Fig. 2c 中对 load 表达式的评估，在对第二个 load 的评估之后，变量 $y$ 可以取值 $r’,t’{1},t’{2}$，研究者引入两个新的布尔变量 $b’ {1}$ 与 $b’ {2}$ 并构建表达式 $(ite\ b’{1}t’{1}(ite\ b’{2}t’{2}r’))$，求解器可以让 $y$ 取如下值：

• 瞬态值 $t’{1}$ ，通过将 $b’{1}$ 设为 true
• 瞬态值 $t’{2}$ ，通过将 $b’{1}$ 设为 false 且 $b’_{2}$ 设为 true
• 常规值 $r$，通过将 $b’{1}$ 与 $b’{2}$ 都设为 false

最后，瞬态值 $t’{1}$ （或是 $t’{2}$） 可以简单地通过将 $b’{1}$ （或是 $b’{2}$）设为 false 来丢弃

0x04. IMPLEMENTATION OF HAUNTED RELSE

本节介绍 Haunted RelSE 的技术细节，主要关注于用以分析 SCT 的二进制级的 RelSE 的变化

由于对数据的依赖项的存在，大部分指令自然地执行或是不能被重排序，其实对于 Spectre-PHT 我们只需要考虑对条件分支的重排序（Section IV-A）并对 Spectre-STL 重排序 load 与 store 即可（Section IV-B）

一个表示为 $\sigma $ 的符号配置（symbolic configuration）由以下组成：

• 当前位置 $l$ ，用以获取程序 $P$ 中的当前指令 $P[l]$
• 符号执行 $\delta $ 的当前深度
• 一个符号寄存器映射 $\rho$ ，将程序变量映射到对应的符号值
• 两个路径谓语 $\pi$ 与 $\widetilde{\pi}$ （具体参见 Section IV-A）
• 一个符号化内存 $\widehat{\mu}$——一对符号数组、其 store 操作的 过期深度 （retirement depth）
• 一组瞬态的 load $\widetilde{\lambda}$ （具体参见 Section IV-B）

记号 $\sigma.f$ 表示配置 $\sigma$ 中的字段 $f$，研究者还定义了一个函数 $eval_expr(\sigma ,e)$ 用以在符号配置 $\sigma $ 中计算一个 DBA 表达式 $e$ 到一个符号值

相比于直接对重排序缓冲区进行建模，研究者使用符号执行的 当前深度 （current depth）来追踪要失效（retired）的指令，一条指令在至多 ∆ 步之后必须要退出，其中 ∆ 为重排序缓冲区的大小；表达式被附注了一个深度以确认其是否要退出，或是其是否依赖于内存，例如寄存器映射 $\rho$ 中的一个变量 $v$ 映射到一对 $(\widehat{\psi},\delta)$ ，其中 $\delta$ 为最近内存访问的失效深度（retirement depth），当 $\delta$ 不需要在上下文中时，其便被省略掉了

A. Haunted RelSE for Spectre-PHT

1) Evaluation of conditional instructions ：与标准的符号执行不同，条件并不会被立刻加入到路径谓语中，而是会与其退出深度一起被保存在一个 推测路径谓语 （speculative path predicate） $\widetilde{\pi}$ 中；当达到一个条件的失效深度时，其会被从推测路径谓语中移除，添加到 失效路径谓语 （retired path predicate） $\pi$ 中

对条件分支的评估如 Algorithm 1 所示，函数首先会评估条件的符号值并确认其可以被安全地泄露，之后其通过更新位置与推测路径谓语 $\widetilde{\pi}$ 以沿着分支 then 计算后续状态 $\sigma _{t}$ 、沿着分支 else 计算后续状态 $\sigma _{f}$

2) Determining speculation depth ：一个条件分支后的推测路径是动态计算的，考虑当其所依赖的所有内存访问都失效时，一个条件可以被完全解出（且预测错误的路径可以被去除），这意味着若该条件并不依赖于内存，则分支并未预测错误

这需要为每个表达式保存其最后内存访问的深度，如 Algorithm 1 所示，在一个条件分支上， $ite\ c\ ?l {true}:l{false}$ 被计算为一个符号值 $\widehat{\varphi}$ 与深度 $\delta$ ，该深度 $\delta$ 被作为条件的退出深度而添加到推测路径谓语 $\widetilde{\pi}$ 中

3) Invalidate transient paths ：在 Algorithm 2 中，条件分支在函数 $retirePHT(\pi,\widetilde{\pi},\delta)$ 中失效，该函数从推测路径谓语 $\widetilde{\pi}$ 中移除所有带有小于当前深度 $\delta _{current}$ 的失效深度 $\delta _{ret}$ 的条件，并将其添加到失效路径谓语 $\pi$ 中，并返回更新后的路径谓语 $\pi$ 与 $\widetilde{\pi}$ ；若 $\pi$ 不可满足，则符号执行将停止

B. Haunted RelSE for Spectre-STL

1) Symbolic memory ：在一个符号配置中，内存 $\widehat{\mu}$ 为从初始内存开始的符号化 store 操作的历史，我们可以使用这个按时间顺序的表示来重新构造 store buffer 与 main memory 的内容；store buffer 也是对符号化内存的最后 |SB| 条未失效 store 的限制，其中 |SB| 为 store buffer 的大小，形式上其被定义为：

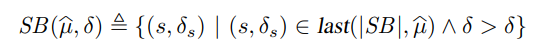
其中 $last(n,\widehat{\mu})$ 为符号化内存 $\widehat{\mu}$ 的最后 $n$ 个元素

类似地， 主存 （main memory）被定义为符号化内存堆失效的 store 操作的限制，形式上定义为 $Mem(\widehat{\mu},\delta)\triangleq\widehat{\mu}\backslash SB(\widehat{\mu},\delta)$

对一个 store 指令的评估如 Algorithm 3 所示，首先该函数会计算下标的符号值并确认其可以在 常规路径谓语 $\pi _{reg}$ 下被安全地泄露（即，失效路径谓语 $\pi$ 与所有 $\widetilde{\pi}$ 中的未决的条件的结合，加上 $\lambda$ 中失效的 transient loads ），接下来其使用一个符号化的 store 操作来更新符号化内存并将该 store 的失效深度设为 $\delta + \Delta$，该失效深度用以确认 store buffer 中的哪一个 store 操作在等待中、哪一个已作用于主存上

2) Evaluation of load expressions ：load 表达式可以通过 store-to-load forwarding 从 store buffer 中获取一个带有匹配地址的未决的 store，也可以推测性地绕过 store buffer 中未决的 store 并从主存取值；相较于考虑一个 load 表达式与 store buffer 中先前所有的 store 之间的交织部分，研究者选用 read-over-write 来辨识与丢弃大部分的 load 与 先前的 store 自然地 commute 的情况； Read-over-write 为一个著名的对数组理论的简化，其在求解器之前解出了符号化数组的 select 操作

为了高效地对比下标，read-over-write 依赖于 语法项等价性 （syntactic term equality），比较函数 $eq^{井} (i,j)$ 仅在 $i$ 与 $j$ 在语法上相等/不等时返回 true/false，若项之间无法进行比较，则为未定义，表示为 $⊥$

公式里的这个 # 不懂为啥老是渲染错误，只能用 井 替代一下：(

为了高效地在求解器之前解出 select 操作，read-over-write 定义了一个依赖于以下语法项等价性的 $lookup _{mem}$ 函数：

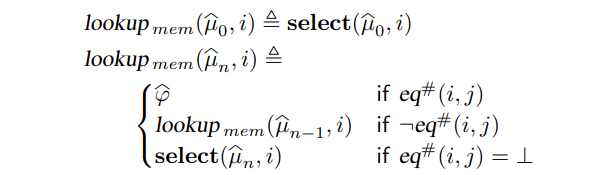
其中 $\widehat{\mu _{n}} \triangleq store(\widehat{\mu} _{n-1} , j, \widehat{\varphi})$

例如考虑这样的一个内存 $\widehat{\mu}$ ：

• $lookup _{mem}(\widehat{\mu},ebp - 8)$ 返回 $\widehat{\varphi}$
• $lookup _{mem}(\widehat{\mu},ebp - 4)$ 首先会比较 $ebp - 4$ 与 $ebp - 8$ 并确认他们是 语义不等的 （syntactically distinct，即 $\lnot eq^(ebp - 4, eax) = \perp$），因此 $select$ 操作并不能被简化

为了高效地建模 store-to-load forwarding，研究者定义了一个 Algorithm 4 中所示的新函数 $lookup _{SB}$，其返回 store buffer 中一组匹配的 store；此外，$lookup _{SB}$ 每个 load 必须要被失效化的深度，即对于相同地址的一个最近的 store 的失效深度

最终研究者定义了 Algorithm 5 中所示函数 $lookup _{ite} (\widehat{\mu},i,\widetilde{\lambda},\delta)$ ，其将 $lookup _{SB}$ 的结果编码为一个符号化的使用新的布尔变量的 if-then-else 表达式；该函数返回 load 表达式的值，并将过程中定义的布尔变量添加到 $\widetilde{\lambda}$ 中；此外，为了实现 $BINSEC/HAUNTED$ ，研究者使用布尔变量的名字来编码关于 load 与前面的 store 的位置的信息；因此，我们有可能使用求解器返回的反例来得知触发漏洞是绕过了哪一个 store，这有助于我们了解漏洞并重构攻击图

对一个 load 指令的评估如 Algorithm 6 所示，首先该函数会计算下标的符号值并确认其可以被安全地泄露，接下来其会调用 $lookup _{ite}$ 获得 load 指令可以取的符号值的集合，编码为一个单独的 if-then-else 表达式 $\widehat{\iota}$ ，并更新 transient load 的集合 $\widetilde{\lambda}$ ；最后其会使用 load 的值更新寄存器映射并将其失效深度设为 $\delta + \Delta$ ；失效深度会在接下来的对条件分支的评估中使用，以确定该条件是否决定于内存

3) Invalidate transient loads ：当更多的最近的匹配的 store 都通过设置对应的布尔变量为 false 而失效了，transient load 的值可以被无效化；于 Algorithm 7 中定义的函数 $retireSTL(\pi,\widetilde{\lambda},\delta)$ 从 transient load 的集合 $\widetilde{\lambda}$ 中移除所有的带有在 $\delta$ 下的失效深度的 load，并在路径谓语 $\pi$ 中将相应的布尔变量设为 false；为了可读性，接下来我们引入一个通过同时使用 $retirePHT$ 与 $retireSTL$ 以停止所有推测的函数 $retireALL$

C. Theorems

本节研究者将证明 Haunted RelSE 对于 SCT 的正确性与完备性（达到一个展开边界），这意味着当 Haunted RelSE 报告了一个违规（violation），其为一个真正的 SCT 违规（没有上近似），且当其在深度 k 上报告没有违规时，该程序在深度 k 上是安全的（没有下近似）；为此，研究者证明了 Haunted RelSE 与 Explicit RelSE 是等价的，且展示了 Explicit RelSE 对于达到一个展开边界（up-to-an-unrolling-bound）的 SCT 而言在上是正确且完备的

Theorem 1. Explicit RelSE 对于达到一个展开边界的推测常数时间而言在是正确且完备的

$Proof(sketch).$ 该证明为一个简单的对 RelSE 对常数时间的正确性与完备性的证明对推测性语义（speculative semantics）的扩展；该扩展需要展示：

• 1）在符号执行中瞬态路径上报告的违规对应到具体瞬态执行中的违规
• 2）若在具体瞬态执行中有一个违规，则在符号执行中有一个路径会报告该违规

接下来研究者将展示 Haunted RelSE 与 Explicit RelSE 等价

Theorem 2. （Equivalence Explicit and Haunted RelSE） Haunted RelSE 检测到了一个违规当且仅当 Explicit RelSE 检测到了一个违规

在 Appendix B 中研究者给出了一个证明草图，其首先展示了 Spectre-PHT 的理论：在一个条件分支后，Haunted RelSE 探索的两条路径完全地获取了 Explicit RelSE 中探索的四条路径的行为；研究者接下来展示 Spectre-STL 的理论：在一条 load 指令之后，Haunted RelSE 产生的单条路径完全获得了 Explicit RelSE 中多条路径的行为

Corollary 1. Haunted RelSE 对于达到一个展开边界的推测常数时间而言在是正确且完备的

D. BINSEC/HAUNTED, a tool for Haunted RelSE

研究者基于二进制级的分析器 BINSEC 实现了 Haunted RelSE 并称之为 BINSEC/HAUNTED ，其获取一个 x86 可执行文件、秘密输入的位置、一个初始内存配置（通常为完全符号化的）、推测的深度、store buffer 的大小作为输入；BINSEC/HAUNTED 以深度优先搜索对程序进行探索，优先处理瞬态路径，并带着反例（即，导致了损坏的初始配置与推测选项）报告 SCT 损坏；其使用当前位向量理论上最好的 SMT 求解器 Boolector

0x05. EXPERIMENTAL EVALUATION

研究者在本论文中回答了这些研究问题：

RQ 1 Effectiveness. BINSEC/HAUNTED 是否能够在真实世界的密码学二进制文件中发现 Spectre-PHT 与 Spectre-STL 损坏？

RQ2 Haunted vs Explicit. Haunted RelSE 与 Explicit RelSE 对比起来如何？

RQ3 BINSEC/HAUNTED vs. SoA tools. BINSEC/Haunted 与最先进的工具比起来如何？

为了回答 RQ1 与 RQ2，研究者对比了 Explicit 与 Haunted 用以关系符号执行的探索策略的性能——两者都应用于 BINSEC/HAUNTED ——在一组真实世界密码学二进制文件与 litmus benchmark（Sections V-B 与 V-C）；为了回答 RQ3，研究者对比了 BINSEC/HAUNTED 与最先进的工具 KLEESpectre 与 Pitchfork（Section V-D）

Legend. 本节中，$I _{x86}$ 为被探索的不同 x86 指令的数量， $P$ 为探索的路径数量，$T$ 为总的执行时间，一个虫子符号 （打不出来）为发现的漏洞数量，⏳为超时数量，✓ 为被证明安全的程序数量，× 为被证明不安全的程序数量

A. benchmark

研究者在一台带有 Intel(R) Xeon(R) CPU E3-1505M v6 @ 3.00GHz 处理器与 32GB 内存的机器上进行实验，除了初始栈指针 $esp$ 以外（类似于related work[5]）所有的输入都是符号的，且数据结构为静态分配的；用户需要标记秘密，其余所有的值都是公开的；研究者将推测深度设置为 200 条指令并将 store buffer 的大小设置为 20 条指令，此外，研究者仅考虑顺序执行中的间接跳转目标并实现了一个 影子栈 以限制返回指令在一个合适的返回位置；考虑瞬态跳转目标需要在任意位置建模间接跳转，对于符号执行而言虽然可行但非常棘手

研究者通过如下程序评估 BINSEC/HAUNTED：

• litmus-pht ：16 个来自于 Pitchfork 的修改过的 Paul Kocher 的 litmus tests 集合的小的测试用例（litmus tests）用以 Spectre-PHT
• litmus-pht-patched ：添加了下标掩码（index masking）的 litmus-pht
• litmus-stl ：新的一组用以 Spectre-STL 的 litmus tests
• 来自 OpenSSL 与 Libsodium 密码学库（详见 Table I） 的密码学原语，包括并扩展至在 [5] 中被分析的那些

程序使用 gcc 10.1.0 编译到 32 位 x86 架构上，litmus tests 被以 -fno-stack-protector 选项进行编译，Spectre-STL 的 litmus tests 额外添加了 -no-pie 与 -fno-pic 以排除由这些选项引入的损坏（参见 Section VI）；由于同一原因，donna 与 tea 不带有 -fno-stack-protector 编译选项，优化级别为 O1、O2、O3 与 Ofast；Libsodium 由默认的 Makefile 进行编译，OpenSSL 开启了 O3 优化，两者都开启了 stack protector

Note on Stack Protectors ：由 stack protector 引入的解决错误的代码非常复杂且包含了许多无法在纯净的符号执行中分析的系统调用，BINSEC/HAUNTED 在系统调用上停止路径执行且每个程序仅跳转到 stack protector 的代码一次，这意味着其可能会错过一些未被探索的代码中的损坏；此外，对于 litmus tests、tea、donna，超时时长被设置为 1 小时，但对于包含 stack protector 的代码则延长至 6 小时（Libsodium 与 OpenSSL）

0x06. NEW VULNERABILITIES AND MITIGATIONS

0x07. RELATED WORK

0x08. CONCLUTION

研究者提出了 Haunted RelSE，一种基于关系符号执行的用以静态检测 Spectre-PHT 与 Spectre-STL 漏洞的技术；特别地，Haunted RelSE 能够通过同时推理常规执行与瞬态执行以显著地减少寻址推测路径的开销；研究者将 Haunted RelSE 应用于一个关系符号执行工具 BINSEC/HAUNTED 中；据研究者的实验结果所示，Haunted RelSE 为迈向可扩展的对 Spectre attacks 的一步；对于 Spectre-PHT，Haunted RelSE 可以在一些情况下极大地提升分析速度，在对中等大小的真实世界中的密码学二进制文件的分析推测语义复杂性进行剪枝；对于 Spectre-STL，BINSEC/HAUNTED 是第一个可以彻底分析真实世界中较小的密码学二进制文件并在中等大小的密码学二进制文件中找到漏洞的工具

最后，研究者通过 BINSEC/HAUNTED，报告了一个标准的对 Spectre-PHT 的防护可以轻易地引入 Spectre-STL 漏洞并提出了修复方法，且发现了一个著名的用于编译位置无关可执行文件的 GCC 编译选项会引入 Spectre-STL