【ALGORITHM.0x02】Dijkstra 算法浅析

本文最后更新于：2026年2月18日 上午

奥利给，干了兄弟们！（指直接用贪心算法）

0x00.绪论

Dijkstra算法算是图论当中最为基础的算法之一，也是各类信息学竞赛（ Olympiad in Informatics ）当中各大图论算法的基础，碰巧今天的离散数学课刚好讲到了Dijkstra算法，所以作为一名蒟蒻·前OIer，今天就来简单讲讲什么是Dijkstra算法XD

不过我当年打OI的时候基本没怎么研究过图论，所以没出过啥成绩XD

Pre. 图的表示

我们首先补充一下 图 这一数据结构的表示方法，首先给出图的定义：

$$
G = (V, E)
$$

其中， G 即为图， V 为顶点的非空有限集合， E 为边的非空有限集合，因此图的定义实际上是 (顶点,边) 的二元组，由此我们有如下的表示图的数据结构：

边表示

由图的定义我们不难想到我们可以直接通过 存储边——节点间连接关系 的方式来表示一张图，例如：

1
2
3
4
5
#include <vector>
#include <utility>

typedef std::pair<int, int> Edge; // start -> end
typedef std::vector<Edge> Graph;

不难看出，使用边来表示一张图是最朴素的基于图的定义进行实现的表示方式，这种方式既可以表示有向图，也可以表示无向图，在表示有向图时，我们通常可以默认定义边的方向是由第一个节点到第二个节点

这种表示方式非常适合稀疏的图

邻接表（Adjunct List）

邻接表 是图的朴素边表示的一种优化，我们注意到原本的表示在针对单个进行查询时一旦相关联的边散落在数组里，则非常容易消耗掉大量额外的时间，因此我们不难想到的是 把每个节点与之相关的边放在一起 ，由此我们就有了 邻接矩阵的表示方式——分开单独记录从某个节点到另一个节点的连接关系，以下是一个例子：

1
2
3
4
5
#include <vector>
#include <utility>

typedef std::pair<int, int> EdgeOut;  // destination, weight
typedef std::vector<std::vector<EdgeOut>> Graph;

邻接表是非常通用的用于存储图的方式，我们会在后面经常见到她 XD

邻接矩阵（Adjunct Matrix）

邻接矩阵表示是另外一种常用的图的表示方式，即定义一个二维数组（二维矩阵）来表示图，当二维矩阵的特定成员值非 0 时即表示 存在一条边 ，例如 g[i][j] != 0 时即表示节点 i 与 j 之间存在一条边（如果是有向图，则通常表示存在一条由 i 到 j 的边）

如果是边带有权值的图，则可以直接使用 g[i][j] 的值表示边的权值

以下是一个例子：

1
2
3
#include <vector>

typedef std::vector<std::vector<int>> Graph;

当然，也可以直接这么表示（毕竟 OI 代码只需要用一次 XD）：

1
2
#define MAX_NODE_NR 0x1000;
int graph[MAX_NODE_NR][MAX_NODE_NR];

这种表示方式对于单条边的查询而言只需要 O(1) 的时间复杂度，比较适合稠密的图，但是缺点在于需要提前分配大量的空间，不适合稀疏的图（会浪费不少内存空间），尤其是对于节点数量较多的图而言，这种二维数组所占用的空间会爆炸式增长（悲）

0x01. 简介：什么是Dijkstra算法？

Dijkstra 算法是由计算机科学家 Dijkstra 提出的基于 贪心 算法的计算非负带权图的单源最短路径的算法，简而言之，Dijkstra 算法会先以某个点作为起始点，并进行如下初始化操作：

  • 定义两个集合：

    • 集合 S ：已经计算了最短距离的点的集合
    • 集合 T ：尚未计算最短距离的点的集合，所有的点在一开始会被放入这个集合

  • 初始化起始点 s 的距离 dist(n) 为 0，初始化所有其他点的距离为 无限大

接下来进行如下循环：

  • 从集合 T 当中选取距离最短的点 n 加入到 S
  • 计算从点 n 出发到其他可直达点（单次设为 m ）的距离 dist(n) + edge(n, m) ，如果这个值小于 dist(m) ，则将 dist(m) 更新为该值，该操作被称为 松弛 （relax）操作

需要注意，对于已经加入 S 的节点，我们不需要反复松弛，因为朴素 Dijkstra 认为到该点的最小距离已被计算，无需额外重复计算

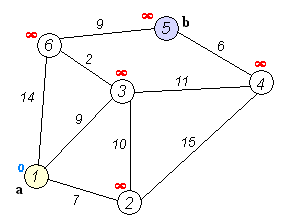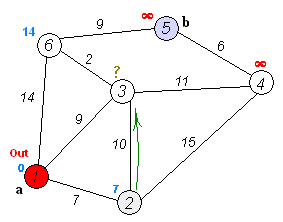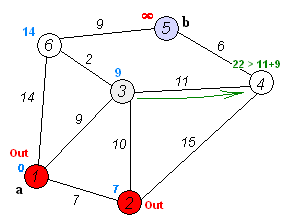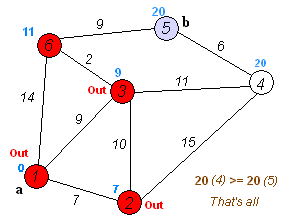
由于起始点的距离被初始化为 0，因此第一次循环必定会选择起始点，由此逐渐扩散到从起始点直达的各个节点，并逐渐扩散下去，下面这张 GIF 很好地表现了这个过程：

从 Wikipedia 偷的

当然，我们注意到这个过程是针对 有向图 的，那么针对 无向图 该怎么解决呢？其实非常简单——

  • 将每一条无向图的边视作两条往返的有向图边即可

示例代码

我们不难看出，由于我们每次都需要对选取的点的所有出边进行遍历，因此 邻接表 在形式上是最适合 Dijkstra 算法的

以下是一份代码例子，输入格式如下：

  • 第一行是四个整数 s, e, n, m ，分别表示起始点、终点、图的点数、图的边数
  • 接下来 m 行每行三个整数 u, v, w，表示图中有一条从 u 到 v 的边权为 w 的有向边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <utility>
#include <vector>
#include <climits>
#include <queue>

typedef std::pair<int, int> EdgeOut;
typedef std::vector<std::vector<EdgeOut>> Graph;

int dijkstra(const Graph& graph, int node_nr, int start, int end)
{
    std::vector<int> dist(node_nr, INT_MAX);
    std::vector<bool> visited(node_nr, false);

    dist[start] = 0;

    for (int i = 0; i < node_nr; i++) {
        int n, min_dist = INT_MAX;
        bool found = false;

        // choose the minimal
        for (int j = 0; j < node_nr; j++) {
            if ((!visited[j]) && (dist[j] < min_dist)) {
                n = j;
                min_dist = dist[j];
                found = true;
            }
        }

        if (!found) {
            break;
        }

        visited[n] = true;

        for (int j = 0; j < graph[n].size(); j++) {
            int m = graph[n][j].first;
            int w = graph[n][j].second;
            if ((!visited[m]) && (dist[m] > (dist[n] + w))) {
                dist[m] = dist[n] + w;
            }
        }
    }

    return dist[end];
}

int main(int argc, char **argv, char **envp)
{
    int edge_nr, node_nr;
    int start, end, shortest;

    // read input
    std::cin >> start >> end >> node_nr >> edge_nr;

    Graph graph(node_nr);

    for (int i = 0; i < edge_nr; i++) {
        int u, v, w;
        std::cin >> u >> v >> w;
        graph[u].push_back({v, w});
    }

    // do dijkstra
    shortest = dijkstra(graph, node_nr, start, end);
    
    // output result
    if (shortest != INT_MAX) {
        std::cout << "Shortest distance is: " << shortest << std::endl;
    } else {
        std::cout << "Destination not arrivable!" << std::endl;
    }

    return 0;
}

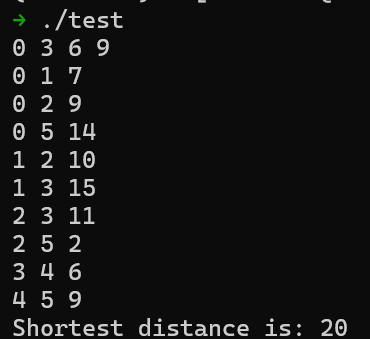
我们用之前的动图作为样例简单测试一下，预期输出是 20：

1
2
3
4
5
6
7
8
9
10
0 3 6 9
0 1 7
0 2 9
0 5 14
1 2 10
1 3 15
2 3 11
2 5 2
3 4 6
4 5 9

成功输出最短距离 20 ：

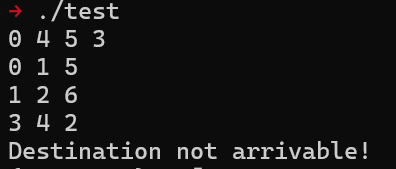
接下来我们构造一个终点不可达的有向图：

1
2
3
4
0 4 5 3
0 1 5
1 2 6
3 4 2

测试，成功输出不可达：

例题：POJ 2387 - Til the Cows Come Home

题目描述

嗯嘛，题目给出 N 个点和 T 条双向边（无向图），让我们找出从点 1 到点 N （题目使用的是 landmark ）的最短路径，简而言之呢，这是非常经典的一道单源最短路问题，因此我们非常容易想到要使用 Dijkstra 进行解决即可

因为题目给的节点是从 1 开始，所以我们构建一个有 N + 1 节点的图，并忽视节点 0 即可

需要注意的是题目是 无向图 ，因此在读取输入时我们应当建立 两节点间的往返的两条边

以及有几个坑点：

  • 题目是先给边数再给点数，注意不要弄反（测试用例非常恶心地给了边数==点数的情况，导致你本地测试的时候不会意识到这一坑点，然后一提交就 WA）
  • POJ 编译器非常老，模板如果有 >> 嵌套，需要写成 > > ，否则会 CE

AC 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <iostream>
#include <utility>
#include <vector>
#include <climits>
#include <queue>

typedef std::pair<int, int> Edge;
typedef std::vector<std::vector<Edge> > Graph;

int dijkstra(const Graph& graph, int node_nr, int start, int end)
{
    std::vector<long long> dist(node_nr, LLONG_MAX);
    std::vector<bool> visited(node_nr, false);

    dist[start] = 0;

    for (int i = 1; i < node_nr; i++) {
        int n, min_dist = INT_MAX;
        bool found = false;

        // choose the minimal
        for (int j = 1; j < node_nr; j++) {
            if ((!visited[j]) && (dist[j] < min_dist)) {
                n = j;
                min_dist = dist[j];
                found = true;
            }
        }

        if (!found) {
            break;
        }

        visited[n] = true;

        for (int j = 0; j < graph[n].size(); j++) {
            int m = graph[n][j].first;
            int w = graph[n][j].second;
            if (!visited[m] && dist[n] != LLONG_MAX && dist[m] > dist[n] + w) {
                dist[m] = dist[n] + w;
            }
        }
    }

    return dist[end];
}

int main(int argc, char **argv, char **envp)
{
    int edge_nr, node_nr;
    int shortest;

    // read input
    std::cin >> edge_nr >> node_nr;

    Graph graph(node_nr + 1);

    for (int i = 0; i < edge_nr; i++) {
        int u, v, w;
        std::cin >> u >> v >> w;
        graph[u].push_back({v, w});
        graph[v].push_back({u, w});
    }

    // do dijkstra
    shortest = dijkstra(graph, node_nr + 1, 1, node_nr);
    
    // output result
    std::cout << shortest << std::endl;

    return 0;
}

0x02. 进阶：Dijkstra 的堆优化

我们注意到在 Dijkstra 算法当中存在一个非常耗时的操作便是 每次执行一个节点都要循环遍历 T 中节点列表找出最小节点，两层的遍历循环直接导致了我们的时间复杂度飙升到 O(N^2 + M)

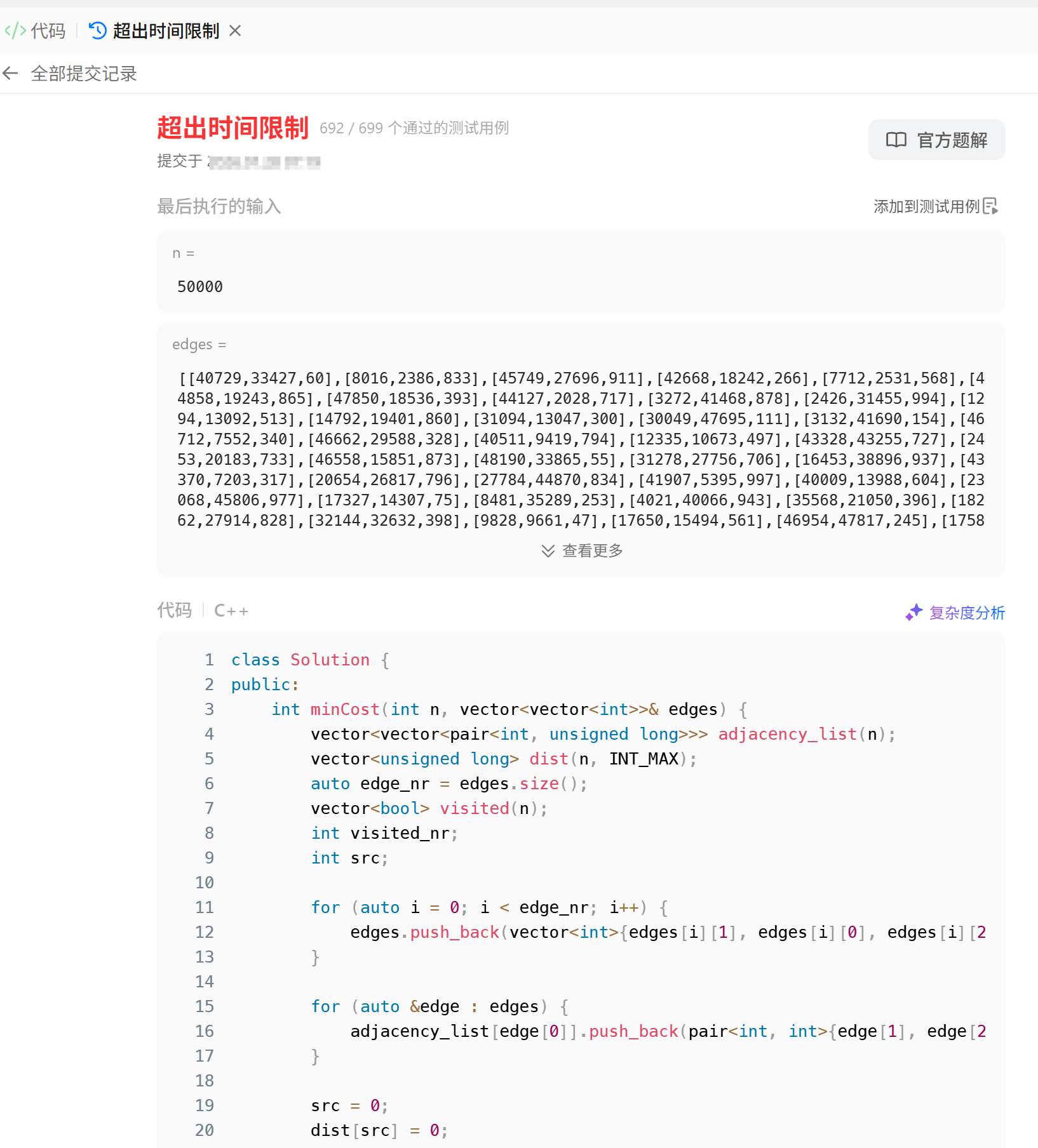
以 Leetcode 的 3650. 边反转的最小路径总成本 为例，这是一道非常朴素的 Dijkstra 无向图的题目，但是给的部分测试点的结构非常大，会导致朴素 Dijkstra 算法 TLE

如何破局？我们不难想到的是——如果我们每次都能直接取出最小节点，我们在这一块的时间复杂度便会大幅降低 ，之后影响时间复杂度的就只是我们的排列操作和遍历每条边的操作

但是我们注意到这个排列操作是需要 动态进行的，因为每一次更新节点都会导致重排序，因此我们需要一个良好的数据结构帮助我们动态维护这样一个排序队列

如何解决这个问题？这就要引入我们的新数据结构——

数据结构：堆

二叉堆（Binary Heap）是一种特殊的 完全二叉树 （除最后一层以外全满的二叉树，且最后一层要么满、要么在右边缺少若干连续节点），其额外满足如下性质：

  • 对于堆中的任意节点 P 与 C ，若 P 是 C 的父节点，则 P 的值小于等于/大于等于 C 的值，此时的堆称为 最小堆/最大堆 （min heap/max heap）

我们将堆的根节点称为堆顶（heap top），底层最靠右的节点称为堆底（heap bottom）

二叉堆的好处在哪？我们注意到， 对于最大堆/最小堆而言，根节点的值总会是堆内的最大值/最小值 ，此外， 二叉堆的插入/删除节点操作会需要维持二叉堆的特性，这保持了根节点总会是堆内的最大/最小值 ——事实上，二叉堆只有根节点的值是会被外部直接使用的，其他节点的值按这个规律放置是为了方便动态插入与删除

这非常适合我们所需要的动态优先队列的数据结构，因此下面我们来看与二叉堆相关的操作

Pre. 二叉树的数组表示形式

通常而言我们比较常用于表示树这个数据结构的自然是链表，比如说：

1
2
3
4
struct TreeNode {
    int val;
    struct TreeNode *left, *right;
};

但是传统的链表形式存在一些缺点，例如两个左右子树指针占用的空间比较多、大量的动态内存分配、离散结构导致的非连续性内存访问造成的 cache miss…

诚然，在绝大部分情况下，我们不得不承认离散的链表形式是不可或缺的，但是其缺点也确乎让人难以忍受，因此我们不禁去想：是否能够优化一下树的存储结构，使其有着优秀的查询访问性能呢？

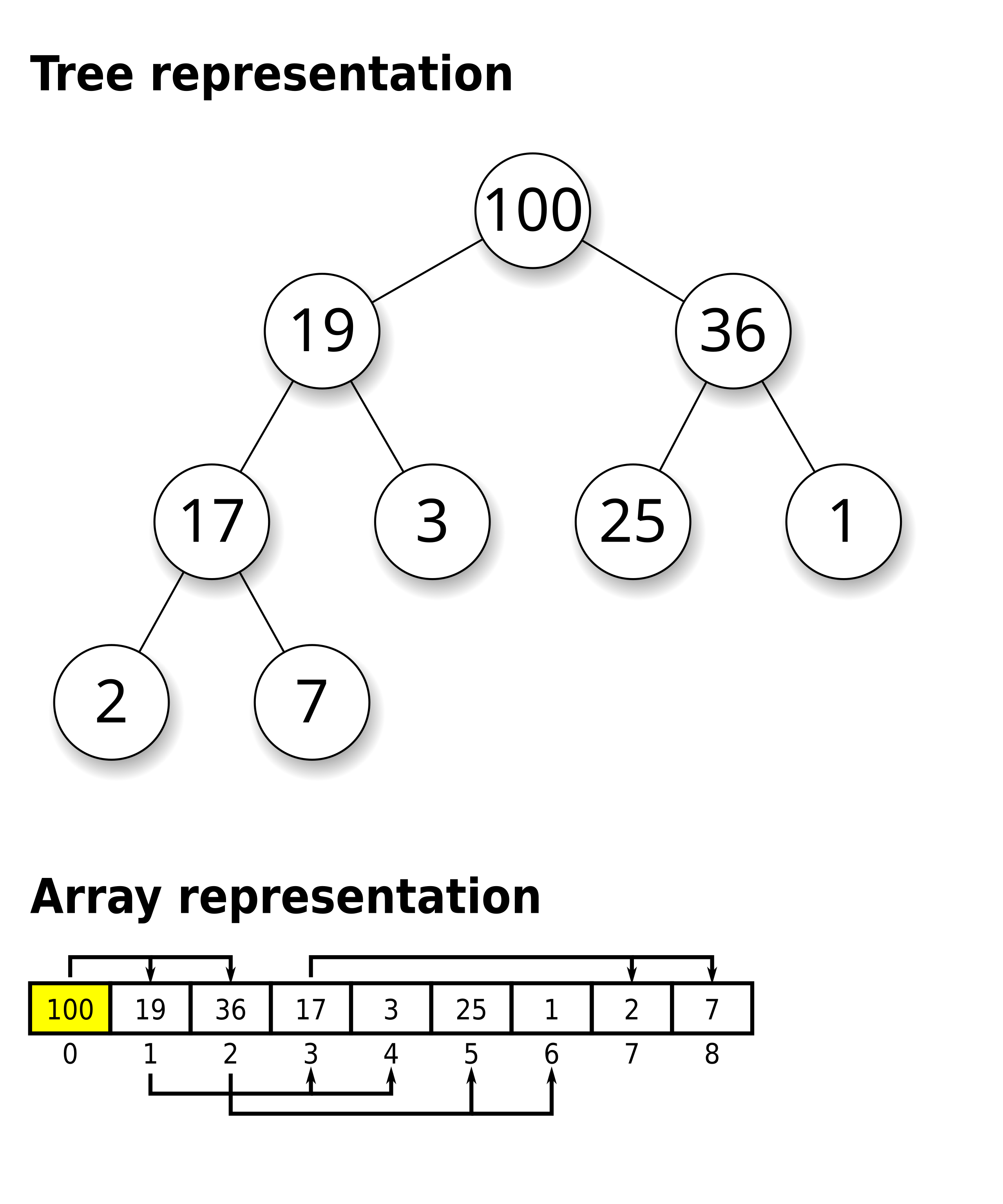
常规的离散的树或许有点困难（当然，我们也可以看到 B Tree 这样有趣的家伙），但是对于 完全二叉树 （Complete Binary Tree）而言，我们注意到其有一个朴素规律或许对我们有所启发：第一、二、三、四、…层的节点数总会是 1、2、4、8、…

——既然每一层的节点数量都是固定的，我直接用一个连续的数组来存放一棵完全二叉树，岂不妙哉？ 由此我们便有了 二叉树的数组表示形式：

1
2
typedef std::vector<int> BinaryTree; // .size() - 1 is the heap end (last element)
// for init, we should fill the [0] as temp

其有着如下特点：

  • 通过数组下标的连续访问，我们可以直接对这棵完全二叉树进行广度优先搜索
  • 我们可以一定程度上节省空间（不需要存储子树指针），且 连续内存访问对 CPU Cache 友好
  • 当根节点下标设为 1 时，我们可以很方便地计算一个节点的亲节点（= i / 2 向下取整 ）与左右子树的下标（左子树 = i * 2 ， 右子树 = i * 2 + 1 ）

由于数组操作十分方便，因此对于 二叉堆 这种树，通常会选择使用数组而非常规的链表来存放

但是对于绝大部分树如红黑树等，实践中还是更惯用链表，其复杂的操作使用指针反而不方便

上浮 / 下沉 操作

在进行插入与删除前，我们先来看二叉堆的两个经典动作：上浮与下沉

  • 上浮 （Swimming）即一个节点在树中不断向上（亲节点）移动（交换位置），直至该二叉树满足最大/最小堆的特性
1
2
3
4
5
6
7
8
9
10
11
void swim_min_heap(BinaryTree &tree, int idx)
{
    while (idx > 1 && tree[idx] < tree[idx / 2]) {
        // swap with parent
        int tmp = tree[idx];
        tree[idx] = tree[idx / 2];
        tree[idx / 2] = tmp;
        // be parent
        idx = idx / 2;
    }
}
  • 下沉 （Sinking）即一个节点在树中不断向下（左或右子树）移动（交换位置），直至该二叉树满足最大/最小堆的特性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void sink_min_heap(BinaryTree &tree, int heap_end, int idx)
{
    while (idx * 2 <= heap_end) { // we have child!
        int target = idx * 2; // left child
        // right child bigger, set as target instead of left
        if ((target + 1) <= heap_end && tree[target + 1] < tree[target]) {
            target = target + 1;
        }
        // no need to swap, just left
        if (tree[idx] <= tree[target]) {
            break;
        }
        // swap with child
        int tmp = tree[idx];
        tree[idx] = tree[target];
        tree[target] = tmp;
        // be the child
        idx = target;
    }
}

插入 / 删除操作

不难看出，插入与删除操作可以基于（需要依赖于）我们前面所定义的两个动作进行实现

插入的实现比较简单，我们可以直接将新的节点创建在堆的末尾 ，之后不断进行 上浮 ，直至亲节点不大于/不小于该节点或是到顶（满足最小/最大堆的特性）

1
2
3
4
5
void insert_min_heap(BinaryTree &tree, int val)
{
    tree.push_back(val);
    swim_min_heap(tree, tree.size() - 1);
}

对于删除而言则稍微有些复杂，首先需要说明的是二叉堆 只允许根节点被删除 （也就是拿出最大/最小节点），因此我们考虑如何在删除根节点后仍旧保持我们的树仍是一个二叉堆

直接删除根节点后我们的二叉堆会变成两棵树，如果要合并两棵树未免有些复杂，很明显我们要在这个过程中尽量避免太多的复杂操作，因此我们不难想到可以 临时将一个节点调度到根节点，之后再不断下沉以他的位置 —— 我们不难想到 堆末尾的节点非常适合担任这个工作，这样我们便无需调整太多节点，只需要将新的根节点不断下沉即可

1
2
3
4
5
6
7
8
9
int delete_root_min_heap(BinaryTree &tree)
{
    int heap_end = tree.size() - 1;
    int res = tree[1];
    tree[1] = tree[heap_end];
    tree.pop_back();
    sink_min_heap(tree, heap_end - 1, 1);
    return res;
}

如何用堆来进行优化？

现在我们已经了解了堆的性质，那么我们该如何使用堆优化查找过程呢？从前面的朴素 Dijkstra 出发，一个比较朴素的思路便是将所有的点维护到一个最小堆当中，每次取出最小的点，遍历其所有的边之后更新目标节点的最小距离

不难发现实际上我们并不需要在一开始就将所有的点都加入到这个最小堆当中（因为除起始点外所有的点的初始距离都被初始化为无限大，这会多出很多无效比较操作），由于一个点的距离在被更新之后才会变为非最大值——此时这个节点的值对我们才是有意义的 ，因此我们可以：

  • 在初始时仅将起始点加入到最小堆中，之后每次循环遍历根节点所能达到的边，若进行了松弛操作则将目标点加入最小堆，直到最小堆中无节点为止

有一个需要注意的地方是我们要比较的是到目标节点的距离，但是交换的是节点编号，因此最小堆的成员值我们应当设为一个 pair ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
typedef std::vector<std::pair<int, int>> BinaryTree; // node, dist

int dijkstra(Graph &g, int node_nr; int start, int end)
{
    std::vector<int> dist(node_nr, INT_MAX);
    std::vector<bool> visited(node_nr, false);
    BinaryTree min_heap(1, {114514, 1919810}); // useless idx 0
    
    dist[start] = 0;
    insert_min_heap(min_heap, {start, dist[start]});
    while (min_heap.size() != 1) {
        int curr = min_heap[1].first;
        delete_root_min_heap(min_heap);
        
        if (visited[curr]) {
            continue;
        }
        
        for (int i = 0; i < g[curr].size(); i++) {
            int next = g[curr][i].first;
            int new_dist = g[curr][i].second + dist[curr];
            if ((!visited[next]) && (new_dist < dist[next])) {
                dist[next] = new_dist;
                insert_min_heap(min_heap, {next, dist[next]});
            }
        }
    }
    
    return dist[end];
}

Tricks：直接使用 std::priority_queue

我们注意到如果在 OI 赛场上每次都要手写这种复杂数据结构，未免太过于耗时，因此 C++ 非常贴心地为我们提供了 std::priority_queue<T> 这一数据结构，其内部实现便是二叉堆：）

例题：洛谷 - U405825 【模板】堆优化 Dijkstra

简而言之，这是一道数据经过特殊构造的 Dijkstra 模板题，题目描述就是朴素 Dijkstra 这里就不搬上来了，我们首先看看如果直接写朴素 Disjktra 会是什么样子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <algorithm>
#include <iostream>
#include <utility>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

typedef pair<int, int> EdgeOut;
typedef vector<vector<EdgeOut>> Graph;

int dijkstra(Graph &g, int n, int start, int end)
{
    vector<int> dist(n + 1, INT_MAX);
    vector<bool> visited(n + 1, false);
    
    dist[start] = 0;

    for (int i = 0; i < n; i++) {
        int curr = INT_MIN, min_dist = INT_MAX;

        for (int j = 1; j <= n; j++) {
            if ((!visited[j]) && (dist[j] < min_dist)) {
                min_dist = dist[j];
                curr = j;
            }
        }

        if (curr == INT_MIN) {
            break;
        }

        visited[curr] = true;

        for (int j = 0; j < g[curr].size(); j++) {
            int next = g[curr][j].first;
            int new_dist = g[curr][j].second + min_dist;
            if ((!visited[next]) && (dist[next] > new_dist)) {
                dist[next] = new_dist;
            }
        }
    }

    return dist[end];
}

int main(int argc, char **argv, char **envp)
{
    int n, m, x, y;

    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m >> x >> y;

    Graph g(n + 1);
    
    for (int i = 0; i < m; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        g[u].push_back({v, c});
        g[v].push_back({u, c});
    }

    cout << dijkstra(g, n, x, y) << endl;

    return 0;
}

简单提交一下，不难看出我们直接 TLE：

因此我们需要使用堆优化来改善我们 Dijkstra 算法过程中最小节点的查找时间，将代码修改如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <algorithm>
#include <iostream>
#include <utility>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

typedef pair<int, int> EdgeOut;
typedef vector<vector<EdgeOut>> Graph;
typedef vector<pair<int, long long>> BinaryTree; // node, dist

void swim_min_heap(BinaryTree &tree, int idx)
{
    while (idx > 1 && tree[idx].second < tree[idx / 2].second) {
        pair<int, long long> temp = tree[idx];
        tree[idx] = tree[idx / 2];
        tree[idx / 2] = temp;
        idx /= 2;
    }
}

void insert_min_heap(BinaryTree &tree, pair<int, long long> new_node)
{
    tree.push_back(new_node);
    swim_min_heap(tree, tree.size() - 1);
}

void sink_min_heap(BinaryTree &tree)
{
    int idx = 1, heap_end = tree.size() - 1;
    while (idx * 2 <= heap_end) {
        int target = idx * 2;

        if (((target + 1) <= heap_end) && tree[target + 1].second < tree[target].second) {
            target = target + 1;
        }

        if (tree[idx].second <= tree[target].second) {
            break;
        }

        pair<int, long long> tmp = tree[idx];
        tree[idx] = tree[target];
        tree[target] = tmp;
        idx = target;
    }
}

void delete_root_min_heap(BinaryTree &tree)
{
    int heap_end = tree.size() - 1;
    tree[1] = tree[heap_end];
    tree.pop_back();
    sink_min_heap(tree);
}

long long dijkstra(Graph &g, int n, int start, int end)
{
    vector<long long> dist(n + 1, LLONG_MAX);
    vector<bool> visited(n + 1, false);
    BinaryTree tree(1, {1, 114514});
    
    dist[start] = 0;
    insert_min_heap(tree, {start, dist[start]});

    while (tree.size() != 1) {
        int curr = tree[1].first;
        delete_root_min_heap(tree);

        if (visited[curr]) {
            continue;
        }

        visited[curr] = true;

        for (int j = 0; j < g[curr].size(); j++) {
            int next = g[curr][j].first;
            long long new_dist = g[curr][j].second + dist[curr];
            if ((!visited[next]) && (dist[next] > new_dist)) {
                dist[next] = new_dist;
                insert_min_heap(tree, {next, dist[next]});
            }
        }
    }

    return dist[end];
}

int main(int argc, char **argv, char **envp)
{
    int n, m, x, y;

    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m >> x >> y;

    Graph g(n + 1);
    
    for (int i = 0; i < m; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        g[u].push_back({v, c});
        g[v].push_back({u, c});
    }

    cout << dijkstra(g, n, x, y) << endl;

    return 0;
}

这个时候我们会发现大部分节点都过了， 但是还有一个节点 TLE ：

如何破局？让我们重新思考我们手写的这个最小堆，我们会发现一些可以优化的点：

  • 在 Dijkstra 中， 当某个点被作为最小距离 Pop 时，其最短路便已经被确定 ，但我们目前的朴素写法仍会在 end 被 Pop 后继续遍历后续的点，这部分操作是无效的
  • 部分节点可能会 重复入堆 （虽然对于重复的点，我们只会使用最小值，这保证了答案的正确性，但是仍然给我们带来不少重复的堆上操作）

现在让我们优化一下这两个点：

  • 我们可以在出堆的节点为目标节点时便结束循环，以减少无效距离计算
  • 在入堆时检查堆中是否已有该节点，若有则直接修改其值，并进行上浮，我们可以使用一个额外的数组维护每个节点的索引

修改后的代码如下（两个点都要改！否则还是会有可能 TLE）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
#include <algorithm>
#include <iostream>
#include <utility>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

typedef pair<int, int> EdgeOut;
typedef vector<vector<EdgeOut>> Graph;
typedef vector<pair<int, long long>> BinaryTree; // node, dist

void swim_min_heap(BinaryTree &tree, vector<int> &idxs, int idx)
{
    while (idx > 1 && tree[idx].second < tree[idx / 2].second) {
        pair<int, long long> temp = tree[idx];
        int tidx = idxs[tree[idx].first];
        
        tree[idx] = tree[idx / 2];
        tree[idx / 2] = temp;

        idxs[tree[idx].first] = idx;
        idxs[tree[idx / 2].first] = idx / 2;
        
        idx /= 2;
    }
}

void insert_min_heap(BinaryTree &tree, vector<int> &idxs, pair<int, long long> new_node)
{
    int target;
    if (idxs[new_node.first] != -1) {
        target = idxs[new_node.first];
        tree[target].second = new_node.second;
    } else {
        target = tree.size();
        idxs[new_node.first] = target;
        tree.push_back(new_node);
    }
    swim_min_heap(tree, idxs, target);
}

void sink_min_heap(BinaryTree &tree, vector<int> &idxs)
{
    int idx = 1, heap_end = tree.size() - 1;
    while (idx * 2 <= heap_end) {
        int target = idx * 2;

        if (((target + 1) <= heap_end) && tree[target + 1].second < tree[target].second) {
            target = target + 1;
        }

        if (tree[idx].second <= tree[target].second) {
            break;
        }

        pair<int, long long> tmp = tree[idx];
        int tidx = idxs[idx];

        tree[idx] = tree[target];
        tree[target] = tmp;

        idxs[tree[idx].first] = idx;
        idxs[tree[target].first] = target;

        idx = target;
    }
}

void delete_root_min_heap(BinaryTree &tree, vector<int> &idxs)
{
    int heap_end = tree.size() - 1;
    idxs[tree[1].first] = -1;
    tree[1] = tree[heap_end];
    idxs[tree[1].first] = 1;
    tree.pop_back();
    sink_min_heap(tree, idxs);
}

long long dijkstra(Graph &g, int n, int start, int end)
{
    vector<long long> dist(n + 1, LLONG_MAX);
    vector<int> idxs(n + 1, -1);
    vector<bool> visited(n + 1, false);
    BinaryTree tree(1, {1, 114514});
    
    dist[start] = 0;
    insert_min_heap(tree, idxs, {start, dist[start]});

    while (tree.size() != 1) {
        int curr = tree[1].first;
        long long curr_dist = tree[1].second;
        delete_root_min_heap(tree, idxs);

        if (curr == end) {
            break;
        }

        if (visited[curr]) {
            continue;
        }

        visited[curr] = true;

        for (int j = 0; j < g[curr].size(); j++) {
            int next = g[curr][j].first;
            long long new_dist = g[curr][j].second + dist[curr];
            if ((!visited[next]) && (dist[next] > new_dist)) {
                dist[next] = new_dist;
                insert_min_heap(tree, idxs, {next, dist[next]});
            }
        }
    }

    return dist[end];
}

int main(int argc, char **argv, char **envp)
{
    int n, m, x, y;

    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m >> x >> y;

    Graph g(n + 1);
    
    for (int i = 0; i < m; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        g[u].push_back({v, c});
        g[v].push_back({u, c});
    }

    cout << dijkstra(g, n, x, y) << endl;

    return 0;
}

成功 AC：

这里其实也可以直接使用 STL 的 priority_queue ，而不是像我们现在这样费劲地手写最小堆，例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <algorithm>
#include <iostream>
#include <utility>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

typedef pair<int, int> EdgeOut;
typedef vector<vector<EdgeOut>> Graph;

struct compare {
    bool operator()(pair<int, long long> a, pair<int, long long> b) {
        return a.second > b.second;
    }
};

long long dijkstra(Graph &g, int n, int start, int end)
{
    vector<long long> dist(n + 1, LLONG_MAX);
    vector<bool> visited(n + 1, false);
    priority_queue<pair<int, long long>, vector<pair<int, long long>>, compare> min_heap;
    
    dist[start] = 0;
    min_heap.push({start, dist[start]});

    while (!min_heap.empty()) {
        int curr = min_heap.top().first;
        min_heap.pop();

        if (curr == end) {
            break;
        }

        if (visited[curr]) {
            continue;
        }

        visited[curr] = true;

        for (int j = 0; j < g[curr].size(); j++) {
            int next = g[curr][j].first;
            long long new_dist = g[curr][j].second + dist[curr];
            if ((!visited[next]) && (dist[next] > new_dist)) {
                dist[next] = new_dist;
                min_heap.push({next, dist[next]});
            }
        }
    }

    return dist[end];
}

int main(int argc, char **argv, char **envp)
{
    int n, m, x, y;

    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m >> x >> y;

    Graph g(n + 1);
    
    for (int i = 0; i < m; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        g[u].push_back({v, c});
        g[v].push_back({u, c});
    }

    cout << dijkstra(g, n, x, y) << endl;

    return 0;
}

也可以 AC，而且还比我们费力手写的更快（悲）：

0xFF. 更多相关题目

Leetcode - 1514. 概率最大的路径

Leetcode - 3650. 边反转的最小路径总成本

洛谷 P1144 最短路计数

ALGORITHM
#C&C++ #Algorithm #Dijkstra #Graph Theory
【ALGORITHM.0x02】Dijkstra 算法浅析
http://example.com/2020/04/23/ALGORITHM-0X02-DIJKSTRA/
作者
arttnba3
发布于
2020年4月23日
许可协议